Введение
В этой заметке приводится решение задачи под номером №19 варианта №38. Задание содержит три спорных утверждения. В ответе следует указать номер верного утверждения.
Вопрос № 1
Верно ли утверждение:
«Касательная к окружности параллельна радиусу, проведённому в точку касания»
Это утверждение было опровергнуто в одной из предыдущих статей:
Значит первое утверждение не верно - в ответ цифру 1 не пишем.
Вопрос № 2
Верно ли утверждение:
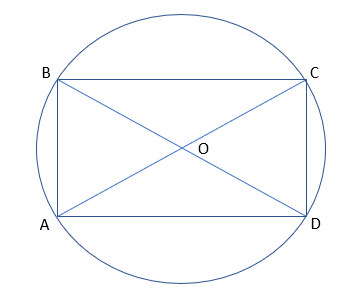
«Любой прямоугольник можно вписать в окружность»
Для доказательства этого утверждения, докажем, что диагонали прямоугольника равны и делятся точкой пересечения пополам.
Равенство диагоналей следует из равенства треугольников
АВD = ВСD (АВ = СD, АD = ВС, ВD - общая).
Диагонали любого параллелограмма, в частности, прямоугольника, делятся точкой пересечения пополам, следовательно
АО = ВО = СО = DО = R – радиус описанной окружности,
то есть окружность радиуса R с центром в точке О пройдёт через все четыре вершины прямоугольника АВСD, что и требовалось доказать.
Итак, второе утверждение верно, и в ответ пишем цифру 2.
Вопрос № 3
Верно ли утверждение:
«Внешний угол треугольника равен сумме его внутренних углов»
Разумеется, этого не может быть, потому что сумма внутренних углов треугольника равна 180˚, а внешний угол меньше 180˚ на величину смежного с ним угла.
Итак, третье утверждение не верно, в ответ цифру 3 не пишем
Ответ: 2
Основные выводы
- Радиус, проведённый в точку касания, не параллелен, а перпендикулярен касательной к окружности.
- Всякий прямоугольник легко вписывается в окружность.
- Внешний угол треугольника равен сумме внутренних углов треугольника, но не всех трёх, а только двух – не смежных с ним.
Желаю новых успехов в подготовке к ОГЭ!


Оставить комментарий