Решение задач ОГЭ по математике: вариант №4 задача №24

Условие задачи

Окружности с центрами в точках P и Q не имеют общих точек, и ни одна их них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры в соотношении а:в. Докажите, что диаметры этих окружностей относятся как а:в.

Решение

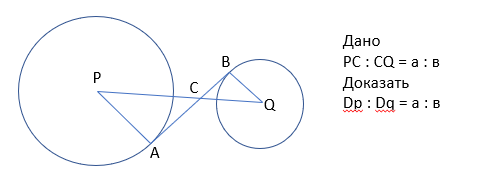
Изобразим ситуацию на чертеже:

Для доказательства достаточно доказать, что половины диаметров - радиусы окружностей относятся, как а:в.

Для этого докажем, что треугольники АРС и ВQС подобны.

Здесь АР и ВQ – радиусы, проведённые в точки касания, которые, как известно, перпендикулярны касательной АВ, следовательно, треугольники АРС и ВQС – прямоугольные.

 Кроме того, ∟ АСР = ∟ВСQ - как вертикальные.

Из равенства углов следует подобие треугольников АРС и ВQС.

Из подобия треугольников АРС и ВQС следует

РС : QС = АР : ВQ = 2АР : 2ВQ = Dp : Dq = а:в

что и требовалось доказать.

Основные выводы

Для решения этой задачи

• нужно построить радиусы окружностей в точки касания и доказать подобие полученных треугольников

Желаю новых успехов в подготовке к ОГЭ!